文本分类
实验概述
【实验目的】
1、通过编程实现基于感知机、K近邻、朴素贝叶斯模型的文本分类模型;
2、通过使用已有SVM工具,通过设计文档的向量表示,实现文本分类。
【实验环境】
(1)软件环境:Python 3.10, Numpy 1.24, nltk 3.8
(2)硬件环境:13-inch, M1, 2020
(3)操作系统环境:macOS Ventura 13.0
(4)网络环境: 校园网ISS-WEB
(5)编程语言:python
【参考资料】
https://blog.datasciencedojo.com/unfolding-naive-bayes-from-scratch-part-1/
https://aiiseasy.com/2019/06/09/text-classification-svm-naive-bayes-python/
https://sebastianraschka.com/Articles/2014_naive_bayes_1.html
https://nlp.stanford.edu/IR-book/html/htmledition/text-classification-and-naive-bayes-1.html
https://www.csie.ntu.edu.tw/~cjlin/libsvm/
https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf
https://zhuanlan.zhihu.com/p/386815121
https://blog.csdn.net/qq_41856733/article/details/106415101
实验内容
【实验方案设计】
数据预处理与统计分析
20Newgroups数据集
20Newgroups数据集由网站http://qwone.com/~jason/20Newsgroups/获得,是用于文本分类的经典数据集,本实验选择的是bydate版本。
该数据集总计18846个文档,已预先分为训练集和测试集,总共有20个类别,每个类别的文本保存在一个目录下。目录结构和文本预览如图1.1.1所示:
图1.1.1
文本向量化
文本向量化的目的是将文本数据转化为数值,从而作为特征向量用于模型训练和分类预测。将每个文档转化为N维特征向量,需要如下几个步骤:
①分词并去除停用词:
分词使用的工具是nltk库中的word_tokenize方法,它可以将英文单词与空格、标点符号分离。停用词包含了常见的英文单词(如代词、冠词、介词、数量词)和一些标点符号,下面的是截取的停用词词典的部分内容如图1.2.1所示:
图1.2.1
这样,我们得到了一个文档中的所有有意义的单词。
②得到所有文档组成的词典:
由于要将文本数值化,因此要将每个单词用一个词项id来表示。方法是得到所有训练集文档的单词,并去重。最后生成一个以词项id为键,单词为值的字典V(|V|=N),并打印到本地txt文件中。本实验生成的字典如图1.2.2所示:
图1.2.2
③根据词典将文档转写成向量
根据得到的大词典,将每个文本文档转成向量,词语按照词项id由小到大排序(为了方便模型算法优化设计),并以txt文件形式保存。保存格式为<词项id,在该文档的出现频次>。本实验的一个文档向量如图1.2.3所示:
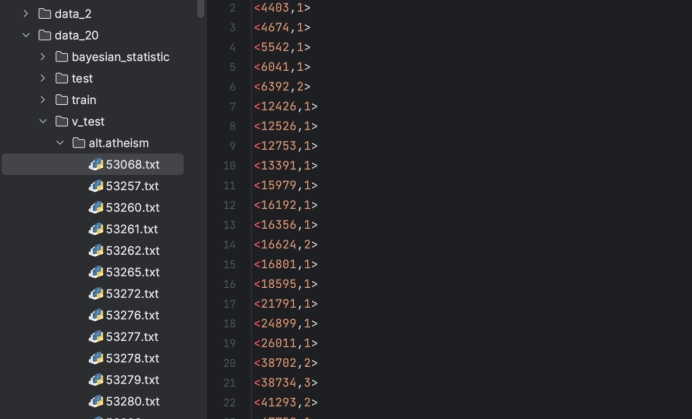
图1.2.3
出于算法优化考虑,本实验的文档存储有如下几个特点:
a、本实验的文档采用稀疏表示,即忽略频次为0的单词,这样可以节省存储空间,减少无谓的计算量。后面会详细介绍这一部分。
b、文档向量的词项根据id从小到大排列,这样在同时处理多个文档时,可以利用单词有序的特性,减少计算量。
c、每个文档向量保存为一个txt文件,并仿照原数据的目录保存,这样做一是为了直观,二是为了保存预处理的结果,方便模型快速处理大量文档向量,而不是从分词开始。
统计每个类的单词的出现次数
文本向量化后,可以训练模型、预测类别,也可以用于其他统计工作。在后面的朴素贝叶斯模型中,需要统计每个类中的每个单词出现的次数,这可以通过把每个文档向量相加得到。在代码实现上,可以把txt文件转换成字典对象,并把键相同的值相加。最后,一共得到20个类别的“向量”,同样,将单词排序后,并用txt格式保存,如图1.2.4所示。
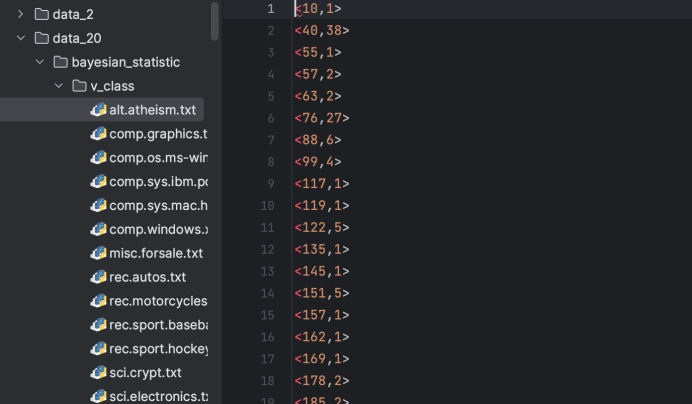
图1.2.4
相关模型
感知机模型
本实验使用单个感知机实现二分类。
首先,用线性方程 来定义超平面 ,其中 是超平面的法向量, 是超平面的截距。这个超平面将特征空间划分为两个部分,从而将位于两部分的点分为正、负两类。如图2.1.1所示:
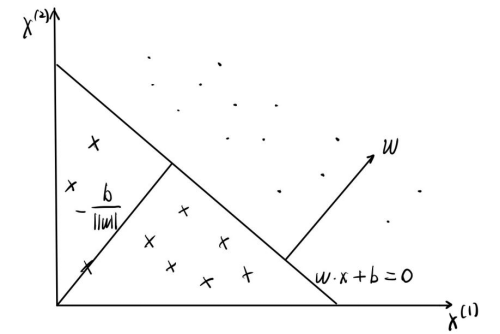
图2.1.1
其次,设损失函数为误分类点到超平面 S的总距离。则损失函数为
目标函数为
对求偏导:
对b求偏导:
采用梯度下降法,随机选取一个误分类点,以的速率进行学习。
若数据集线性可分,则,最终收敛于常值,此时损失函数最小。但由于大部分数据不是线性可分的,因此本实验不能保证和最终趋于常数,因此需要循环迭代。循环次数人为给定,并和学习率一同作为超参数进行模型性能分析。
在本实验中,仍然采用N维文本向量,而每一维的数值采用TF-IDF值,这样可以提升稀有单词的权值,使得分类更高效。TF-IDF的计算采用以下公式:
其中,表示词条在文档中出现的次数,表示所有文档的数量,表示词条的文档数量。
K近邻模型
K近邻算法(K-Nearest Neighbor,KNN)是一种基本的分类算法,它从训练数据中选择K个最近邻近数据作为输入的测试数据的分类。
具体来说,KNN算法通过计算测试数据与各个训练数据之间的距离来确定最近邻近的K个样本。距离可以使用欧氏距离,曼哈顿距离和闵可夫斯基距离等测量方式。然后将K个最近邻的标签进行比较,将测试样本分配到类别中最常见的类中。因此,KNN算法不需要实际训练过程,只需要对训练数据进行存储和计算距离。
KNN算法在特征空间中的距离测量和分类决策上采用了非参数方法,没有对判定函数进行假设,不需要预先假设数据的分布情况,可以适用于任何数据分布。因此,KNN算法是一种懒惰算法,有很好的优点,但它的缺点包括预测效率低下和需要大量的存储空间。
在KNN算法中,K值的选择很重要。如果K值太小,会使模型过拟合;如果K值太大,会使模型欠拟合。在训练过程中,一般采用交叉验证的方法,通过比较不同的K值,在测试集上选择具有最小误差的K值。
总之,KNN算法是一个简单而易于实现的算法。尽管它有一些缺陷,但它仍然是机器学习中重要和受欢迎的算法之一。过程如下:
- 初始化输入测试数据,K值,以及距离衡量指标。
- 对于每个测试样本,遍历所有训练数据,计算测试样本与训练数据集之间的距离。
- 根据距离测量指标,将训练数据集按照距离递增的顺序排序。
- 选取距离测试样本最近的K个训练样本数据。
- 分析K个训练样本数据中出现最频繁的类别并将其作为测试样本的预测类别。
- 返回预测的测试样本的类别标签。
在本实验中,每一个训练集中的文档都是N维向量,也被视作N维空间的点。每个测试文档也是该空间中的一个点,通过计算距离其最近的k个点,找到个数最多的类别,就能预测其类别。本实验将k作为超参数分析模型性能。
需要注意的是,由于文档向量的稀疏性,其99%以上的词项频率都是0。因此在计算距离的时候,为了节约计算时间,不预先把文档表示成N维,而是利用词项的有序性,把测试向量和与之计算距离的训练向量进行逐维比较。具体方法在下一节介绍。后续的实验证明,这样一种“形似”N维的计算方法是高效的。
另外,sklearn的k近邻算法API为KNeighborsClassifier()。
朴素贝叶斯模型
朴素贝叶斯法是一种基于贝叶斯定理与特征条件独立假设的分类方法。其中朴素指的就是条件独立。朴素贝叶斯在分类的时候不是直接返回分类,而是返回属于某个分类的概率。 例如对文章的类别进行判断,如图3.3.1所示:

图3.3.1
朴素贝叶斯算法计算出的是每篇文章属于某个类别的概率,哪个类别占的比例比较大,则将文章归为哪一类。简单地说,朴素贝叶斯是根据概率的大小进行分类。
其次,朴素贝叶斯需要用到一些概率知识,即联合概率和条件概率。
联合概率:包含多个条件,且所有条件同时成立的概率。
条件概率:事件A在另一个时间B已经发生条件下的概率。
但是需要注意上述的求概率公式只适用于各个特征之间是条件独立(每个特征之间没有必然关系)的情况。
此外,sklearn提供了三种不同类型的贝叶斯模型算法:高斯朴素贝叶斯、多项式朴素贝叶斯和伯努利朴素贝叶斯,因为本次实验选择多项式朴素贝叶斯,所以仅介绍该算法。
多项式朴素贝叶斯主要适用于离散特征的概率计算,且sklearn的多项式模型不接受输入负值。 若处理连续性变量要选择高斯模型。多项式朴素贝叶斯多用于文档分类,它可以计算出一篇文档为某些类别的概率,最大概率的类型就是该文档的类别。举个例子,比如判断一个文档属于体育类别还是财经类别,那么只需要判断P(体育|文档)和P(财经|文档)的大小。而文档中其实就是一个个关键词(提取出的文档关键词),所以我们需要计算的P(体育|词1,词2,词3…)和P(财经|词1,词2,词3…)。我们之前求得都是一个条件下多类别的公式,例如P(A1,A2|B)=P(A1|B)P(A2|B)。而我们现在求的是多个条件一个类别,那么该如何求呢?这就需要用到朴素贝叶斯公式:
W为给定文档的特征,也就是文章中拆分出来的不同词语,C为文档的类别(财经,体育,军事…) ,因为文档中要提取关键词,所以也可将公式理解为
最后,当某个词不出现时,会导致概率为0。由于不能因为一个词不出现而否定了其他关键词,所以需要引入拉普拉斯平滑系数:
为指定的系数,一般为1,m为训练文档中统计出的特征词个数。这样就不会出现概率等于0的情况了。
另外,sklearn的朴素贝叶斯API使用方式如下:
1 | MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None) |
SVM模型
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如图2.4.1所示, 即为分离超平面,对于线性可分的数据集来说,这样的超平面有无穷多个(即感知机),但是几何间隔最大的分离超平面却是唯一的。

图2.4.1
线性支持向量机学习算法如下:
输入: 训练数据集,其中,,;
输出: 分离超平面和分类决策函数。
(1)选择惩罚参数C>0 ,构造并求解凸二次规划问题。
得到最优解。
(2)计算
选择的一个分量满足条件,计算
(3)求分离超平面
分类决策函数:
本实验使用sklearn提供的支持向量机工具来执行二分类任务。Sklearn已经提供了一套数据预处理的方式,并且内置读取数据、评估模型的方法,十分方便。我们把核函数类别和惩罚项C作为超参数,进行模型性能测试。
惩罚项C越大,即对分错样本的惩罚程度越大,因此在训练样本中准确率越高,但是泛化能力降低,也就是对测试数据的分类准确率降低。相反,减小C的话,容许训练样本中有一些误分类错误样本,泛化能力强。
核函数包括线性核函数(‘linear’)、多项式核函数(‘poly’)、高斯核函数(‘rbf’)等,本实验将使用这三种核函数进行测试。
算法实现
项目介绍
程序框架如图3.1.1所示:
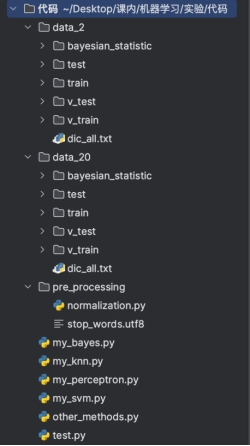
图3.1.1
其中,test是测试代码包含对每个模块的调用,以及参数的设置,代码如下:
1 | my_bayes.naive_bayes_test(which_data='data_20', lamb=0.2) |
文件夹pre-processing下存放用于预处理的代码和文件;
data_2和data_20分别是用于二分类和二十分类的数据集目录,包含已经向量化的所有文档(v_train和v_test)、词典文件(dic_all.txt),以及包含贝叶斯所需统计量的目录(bayesian_statistic);
my_bayes.py,my_knn.py, my_perceptron.py和my_svm.py是四个模型的实现代码,都封装为方法,以便直接调用。
other_methods.py是使用sklearn中其他的工具,进行文本分类的尝试。
模型实现是本实验的核心部分,下面将选取核心算法部分进行说明。
感知机算法
①文档的TF-IDF表示:
文档的TF-IDF是同时进行读取和计算。计算过程分成两步,第一步是得到V中所有单词的逆文档频率idf,存入一个词典:
1 | def get_idf(): |
第二步是生成文档向量,该向量的每一维不再是单词的文档频率,而是:单词的tf-idf = 单词的文档频率 tf * 单词的逆文档频率idf:
1 | def get_d_array(path, V): |
②梯度下降调整和
生成的文档向量采用N维np数组表示,向量也由N维np数组表示,初始化为0,偏置量b也初始化为0。
根据第二部分设计的损失函数,对每一对误分类实例,调整和
由于训练集线性不可分,所以和无法自动收敛,需要人工定义循环次数多次从而迭代调整,以达到趋于常数的目的。循环次数为我们传入的参数max_iter,每次循环遍历所有训练集。此外,本实验采用在线学习(online learning)的形式,若遇到实际标签和预测标签(标签被定义为1和-1)异号,则立刻调整和。使用numpy内置的multiply,add和dot方法可以很方便地实现算法:
1 | w = np.zeros(len(V)) # w是|V|维向量,初始化为全0 |
③预测文本类别:
1 | def perceptron_predict(w, b, d): |
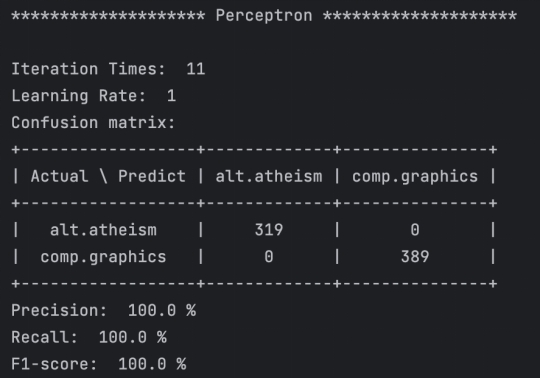
图3.2.1
K近邻算法
①距离计算
由于是稀疏表示的向量,可以用更高效的方式计算距离。方法是维护一个dis变量,设置两个指针分别从两个向量的第一个词开始比较词项id大小,不相同则表示更大的词项所在向量的该维度数值为0,因此只需要计算id更小的词项对应数值自身(若p为2,则是乘方),并加到dis上;若遇到相同的id,则代表两个向量该维度数值非0 ,需要相减再处理,并加到dis上:
1 | def get_dis(d, t, p): |
②多数表决
该方法是将所有训练样本与文档vd的距离由小到大排序,并用argsort()记录索引。K近邻则取前k个索引,以及它们各自的标签,存入predict_class列表。再使用counter.most_common方法统计出现次数最多的类:
1 | sorted_index = dis.argsort() |
运行结果如图3.3.1所示:

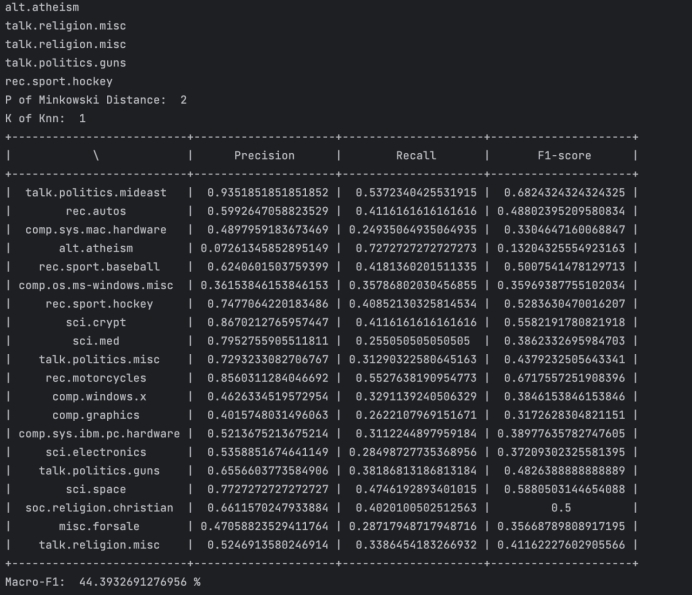
图3.3.1
朴素贝叶斯模型
①计算先验概率
对每个类向量,调用一个get_sum_words方法,统计该类所有单词出现次数的总和Nc。将每一类的Nc求和,得到所有文档的词数N,Nc/N即可得到每个类的先验概率prior。将结果存储在列表中,并保存为prior.txt文件,如图3.4.1所示。
1 | from_path = which_data + '/v_train' |
图3.4.1
②计算各单词在各类的频率
定义一个二维数组condprob,对每个类,遍历V中所以的单词,计算单词在该类下出现的频率。
1 | condprob = [[0 for i in range(len(C))] for j in range(NV)] |
③计算后验概率并最大化
对于测试文档vd,计算其每个类下的后验概率,计算方式为将vd下的每个单词的频率取对数相加(等效于将频率求积),这样可以防止小数点因为数据精度过大被自动舍去。最后加上该类的先验概率的对数,得到一个类的后验概率,保存在score列表中。score中数值最大元素的索引,即是预测类别:
1 | for c in C.keys(): |
运行结果如图3.4.2所示:
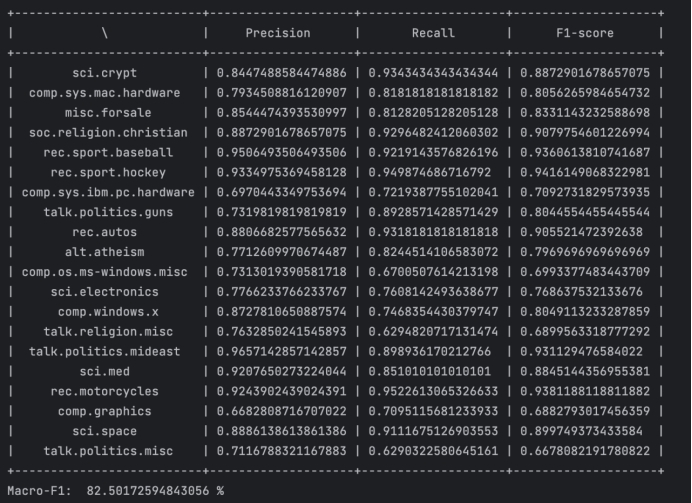
图3.4.2
支持向量机
①获得训练和测试数据
1 | train = fetch_20newsgroups(subset='train', categories=category) |
②支持向量化
向量化使用sklearn内置的TfidfVectorizer模块,生成tf-idf向量:
1 | vectorizer = TfidfVectorizer() |
③训练模型
训练模型使用model.fit方法,最后得到预测标签和实际标签两个列表:
1 | model = SVC(C=C, kernel=kernel) |
(6)评价方法
本实验的模型评价方法是Macro-F1,这部分的代码实现以贝叶斯模型为例。
首先需要得到每个类别的F1指标,F1指标需要先计算精准率和召回率,这里采用三个词典t,f,p,分别存放每个类别被正确预测的文档数量、被错误预测的文档数量、预测的其他每个类的数量。对于类别i,计算recall(i) = t[i]/(t[i]+f[i])可以得到召回率,计算precision(i) = t[i]/(t[i] + p[i])可以得到精准率。
1 | t = {}.fromkeys(range(len(C)), 0) |
然后,计算每个类别的F1指标,计算公式为。Macro-F1假设每类权重相同,因此Macro-F1=ΣF1/|C|。
1 | precision = {} |
运行结果如图3.5.1所示:
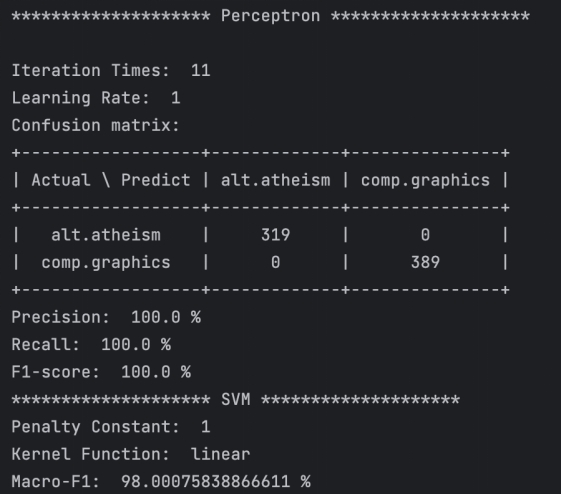
图3.5.1
其他模型
1、导入十种模型
1 | from sklearn.naive_bayes import MultinomialNB **#朴素贝叶斯** |
2、将文章数据向量化(TF-IDF算法)
1 | select = ['alt.atheism','comp.graphics','misc.forsale','rec.autos', |
3、准备循环遍历的分类器
1 | Classifier = [MultinomialNB(),DecisionTreeClassifier(),KNeighborsClassifier()] |
4、将函数分为四组进行输出
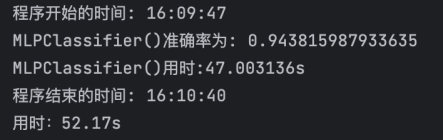

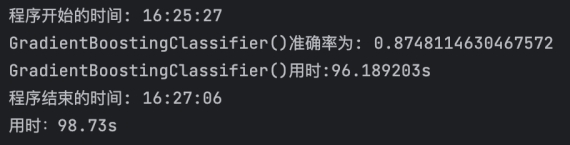
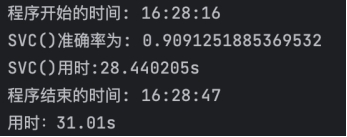
整理结果如下,按照准确率从高到低,运行时间由短到长进行排列。
准确率:多层感知机(0.944)、随机梯度下降(0.941)、逻辑回归(0.916)、支持向量机(0.909)、梯度上升(0.877)、朴素贝叶斯(0.871)、随机森林(0.856)、k近邻(0.808)、Ada(0.765)、决策树(0.732)
运行时间:朴素贝叶斯(0.01)、随机梯度下降(0.07)、k近邻(1.02)、决策树(1.66)、逻辑回归(2.86)、Ada(3.35)、随机森林(3.59)、支持向量机(29.14)、多层感知机(47.00)、梯度上升(96.66)
各文本分类模型的超参数敏感性分析
本实验分别对每个模型选取了一些典型的超参数,并选定合适的区间进行实验,绘制了如下Macro-F1 Score折线图。
感知机
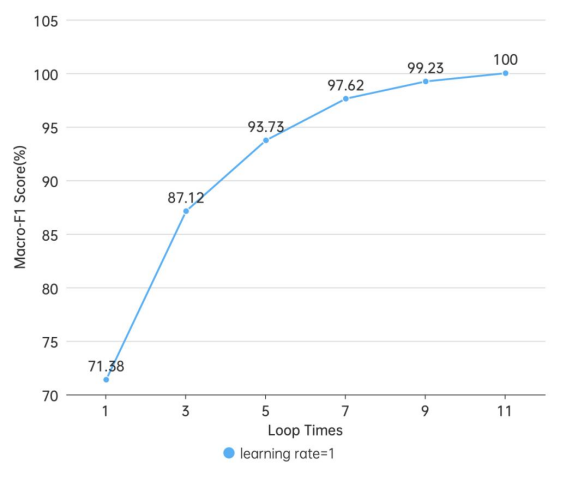
本实验感知机的每次调整读取一个文档。由图可知,随着循环次数的增加,模型评分也逐渐增加,并且当次数大于5次后,增势趋缓;在循环11次后,模型的评分达到了100%,即全部预测正确。
实验还发现,学习率对模型的得分没有影响,因此只选取学习率为1的模型进行分析。
KNN
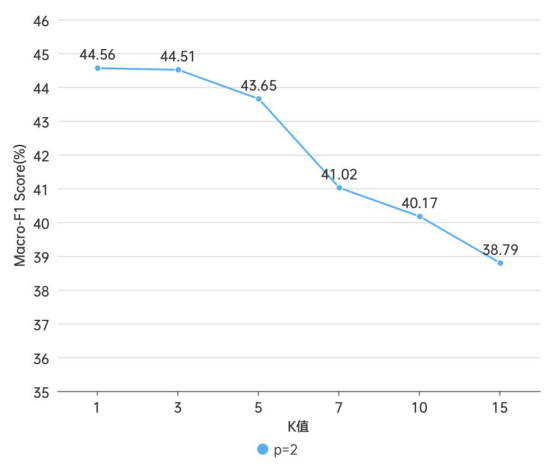
本实验只测试了p值为2时的KNN模型。由图可知,模型的表现随K值的增大而下降,在K=1时模型表现最好,Macro-F1为44.56%;在K=3时为44.51%,变化不大;之后随着K值增大,评分迅速下降,当K大于7后,下降速率减缓。
朴素贝叶斯
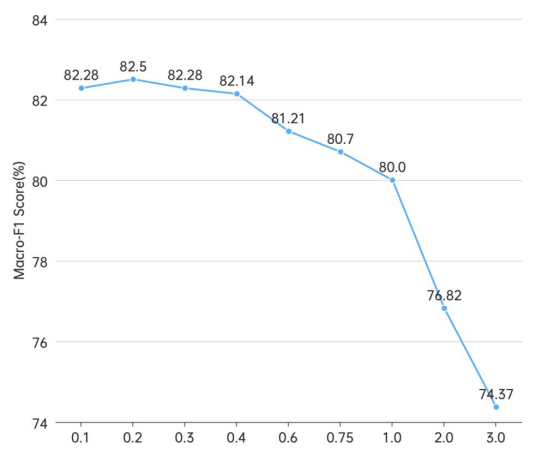
由图可知,当λ在0.1-0.5之间,模型Macro-F1得分较高,其中λ=0.2时达到峰值82.5%;之后,随着λ增加,Macro-F1得分线性递减。特别地,在λ=1时,模型的准确率为80.0%。
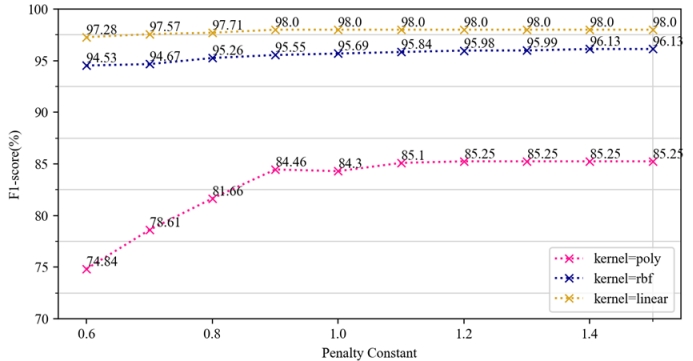
支持向量机
本实验选取了三种核函数,分别是多项式核函数、高斯核函数和线性核函数。对每个核函数,测试在惩罚系数为0.6-1.5时的模型表现,得到下图。
由图可知,在处理二分类问题时,线性核函数表现最好,高斯核函数次之,两者得分都能稳定在95%之上,而多项式核函数的表现最差,最优设置下的得分仅有85%左右。三个模型的得分都随着惩罚系数增加而提升,并且最终收敛于常数。
结果分析
在处理二十分类问题时,贝叶斯算法的效果比KNN更好**。在最优设置下,贝叶斯的Macro-F1得分为82.50%,而KNN得分为44.46%;**感知机和SVM在处理二分类问题时效果都非常好,在使用TF-IDF文档向量表示时,感知机评分高达100%,SVM则高达98%。
此外,在调用的十种方法中,多层感知机的准确率最高,达到了0.944,但速率较慢,用时47s;运行时间最短的是朴素贝叶斯,用时0.01s,准确率排在中间,为0.871。可见一种算法往往很难兼顾准确率和运行效率。
小结
本次实验是我第一次自己尝试动手实现机器学习算法,虽然一开始感觉算法实现有些复杂,但通过阅读助教分享的代码、请教同学以及上网查询资料等过程,我逐渐理清了头绪,最终通过三周的学习与尝试,为本次实验画上了一个比较满意的句号。
首先,在机器学习算法的理解方面,最初通过课本知识的学习,我有了一个基本的了解,但通过自己动手,才真正对感知机、KNN和贝叶斯三个模型有了更深刻的了解。比如,在感知机模型中,因为w和b往往不能自动收敛,所以需要循环训练来达到近似收敛的效果;在KNN模型中,构建KD树与否直接决定了模型的计算效率。
其次,在模型的应用方面,我尝试了对文本数据进行预处理,并将模型应用于现实生活的情景。通过多个模型的使用,我发现没有最好的模型,只有最合适的模型。在不同问题下,选用不同的模型,才能得到最好的效果。例如,文档向量的TF-IDF表示和词袋表示就能产生不同的效果。
最后,我的代码能力也得到了很大的提升。在这次实验过程中,我思考了如何提升数据读取和存储的效率,如何应用不同的方法解决问题,如何让代码保持良好的可读性等等问题,这个过程使我的代码实现能力得到了很大的提升。
总而言之,本次实验我收获良多,为将来的学习打下了重要的基础。



